Reaching for the known unknowns: Rapid reach decisions accurately reflect the future state of dynamic probabilistic information
Wispinski, N. J., Stone, S. A., Bertrand, J. K., Zuk, A. A. O., Lavoie, E. B., Gallivan, J. P., & Chapman, C. S. (2021). Reaching for known unknowns: Rapid reach decisions accurately reflect the future state of dynamic probabilistic information. Cortex, 138, 253-265.
Let’s use a Canadian example. Imagine you are a hockey forward on a breakaway. You are skating with the puck, and only the goalie stands in your way. The goalie shifts to the left and to the right, getting ready for you to shoot on net. Time is up—where do you shoot?

To score a goal, you need to make a prediction. You need to calculate where to shoot based on where the goalie will (and will not) be in the future. What makes these actions even more impressive is the capacity of the brain to account for various delays in the nervous system. When I show you an image, it takes some time for your brain to process it. And when you want to make an action, it takes some time for you to execute that action. Transforming vision into action takes time.
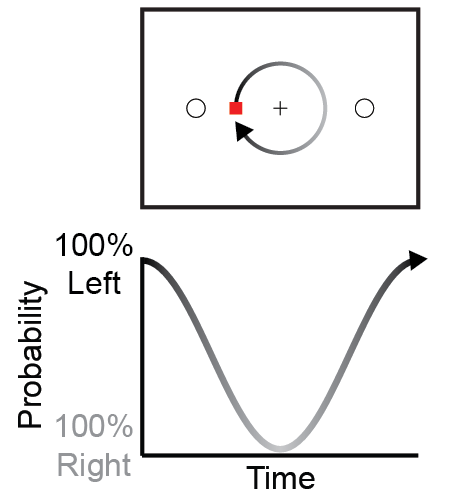
Here is an experiment that tries to get at this complex behaviour. Your hand is on a start button in front of a screen. A red box rotates clockwise, counterclockwise, or stays still. There are two circles on the screen. When you hear a beep, you need to reach and touch the circle that fills in.
And you need to reach fast.
The catch? The probability that you need to touch the left or right circle depends on where the box is when you lift your hand off the start button. If the box is next to the left circle, there is a near 100% chance that you will need to touch the left circle. If the box is halfway between the left and right circles, there is a 50% chance you will need to touch either the left or right circles.
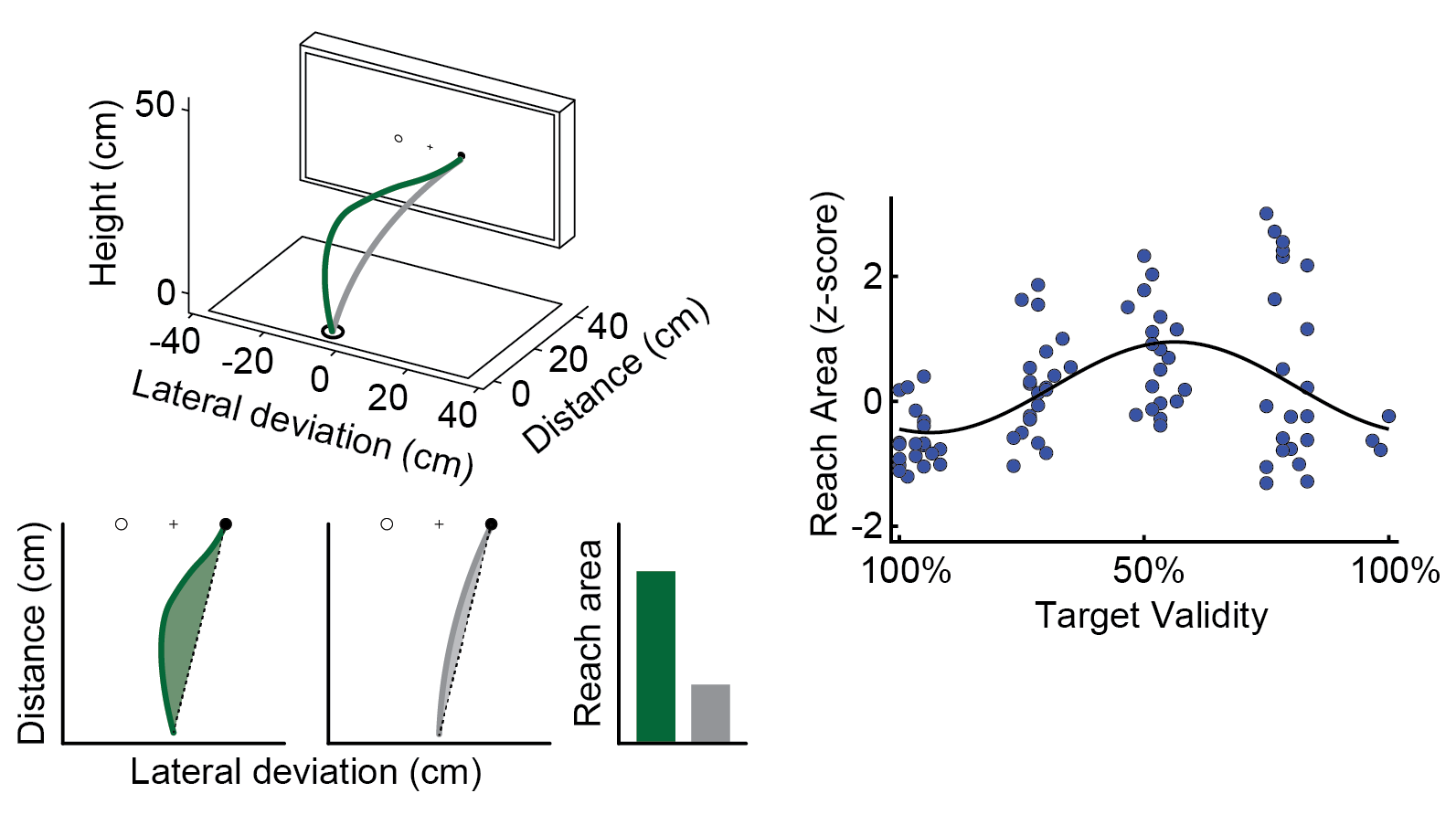
Below is a trial slowed down, with a participant’s reaching movements reconstructed. We used an infrared motion tracking system to record the hand position of each participant 150 times per second.
We were especially interested in reach area—or how curved movements were when you went to touch the screen. Many researchers think that when you are more confident in your decision, you move more directly to where you want to go, and when you are less confident, you move less directly.
Because the box moved in a circle, the probability of the left and right targets being filled in changed over time like a sine wave. It turns out participants in our experiment behaved in a sine wave-like manner as well.
To make these data simpler to analyze, we fit a sine wave to each participant’s measures of reach area (how curvy you moved) and accuracy (if you touched the correct circle) on all of the trials that they completed. We can then see if the sine wave fit to behaviour matched the sine wave of the rotating box.
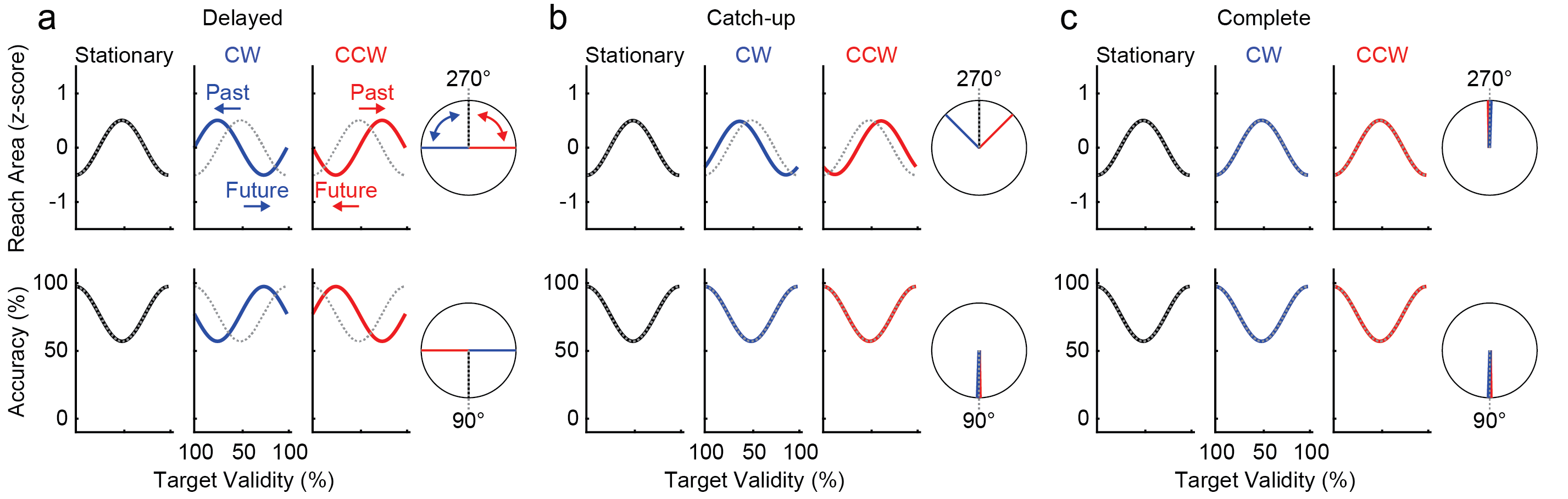
We had 3 predictions in this paper.
First, people’s behaviour might be delayed. If we looked at how people moved, and which circle they tended to touch, these measures would reflect the box position some time in the past. The sine waves fit to people’s behaviour would be behind the sine wave of the rotating box.
Second, people’s behaviour might be initially delayed, but they would use the little bit of extra time while moving their arm to update their predictions.
Third, people might just be really good at predicting how likely the left and the right circles would fill in. This suggests that people know exactly how long it takes for them to start moving after the beep, and are behaving as if the box was that far ahead of where it actually was. They are effectively living in the future. In this case, the sine waves fit to people’s behaviour would exactly match the sine wave of the rotating box.
Below are what the sine waves for reach area and accuracy would look like under each of these predictions.
We found exactly the third possibility. Below are the sine waves fit to the behaviour of each of the people who participated in this study (in grey), and the average of all the participants (in colour). The sine waves match up very well with the sine wave of the rotating box (dashed lines).
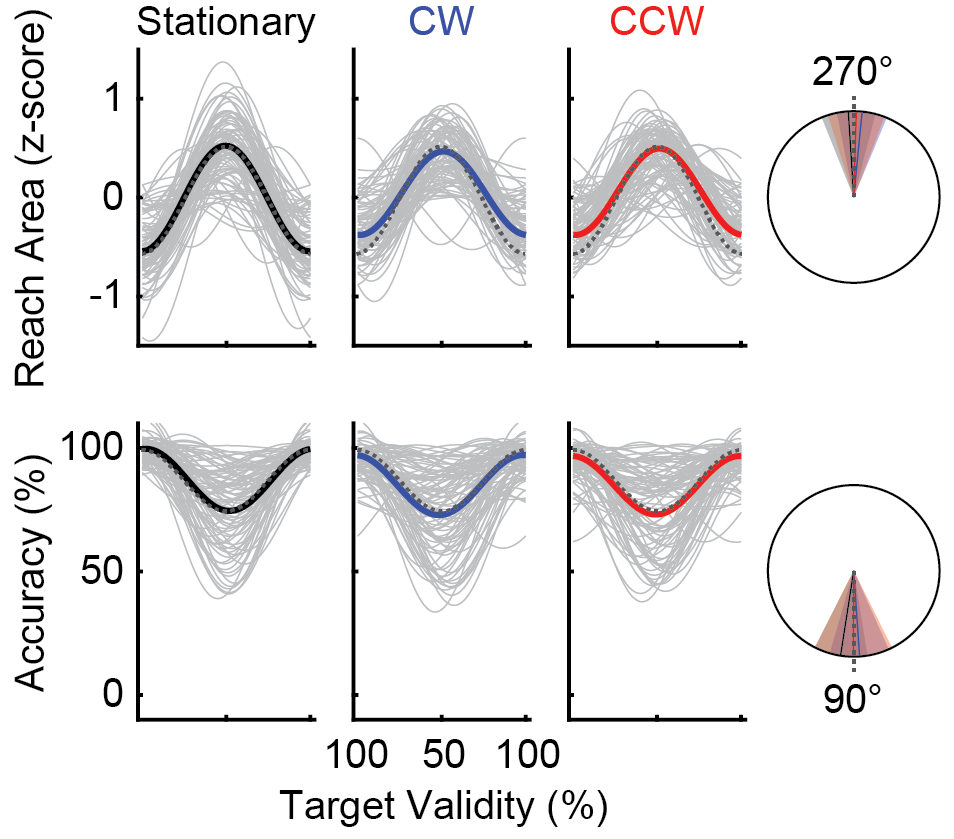
It turns out, humans are very good at quickly and accurately integrating their predictions with estimates about delays in their own brains and bodies to effectively guide action. The results of these experiments speak to one key part of how humans are able to carry out actions in complex and dynamic environments, from touching a circle on a screen, to scoring a goal on a breakaway.
